Restas prestando

Unidades y decenas (Matemáticas)

Sumas llevando (Segundo)

Principio de la multiplicación

Da click en el siguiente vínculo: 


Principio de la multiplicación

Números decimales (Matemáticas tercero)

Hasta ahora hemos trabajado con números enteros, cuya cifra más pequeña es la unidad:

  

Pero también hay número que tienen una parte inferior a la unidad, estos se llaman números decimales:

Los números decimales se utilizan para representar números más pequeños que la unidad. 

La parte entera va a la izquierda de la coma y la parte decimal a la derecha.

Vamos a ver cada una de estas cifras decimales.

a) La décima

La décima es un valor más pequeño que la unidad

1 unidad = 10 décimas.

Es decir, si dividimos una unidad en 10 partes iguales, cada una de ellas es una décima.

Las décimas van a la derecha de la coma.

b) La centésima

Es un valor más pequeño que la unidad y también que la décima.

1 unidad = 100 centésimas

1 décima = 10 centésimas.

Es decir, si dividimos una unidad en 100 partes iguales, cada una de ellas es una centésima.

Y si dividimos una décima en 10 partes iguales, cada una de ellas es una centésima.

c) La milésima

Es un valor más pequeño que la unidad, que la décima y también que la centésima:

1 unidad = 1.000 milésimas

1 décima = 100 milésimas

1 centésima = 10 milésimas

Es decir, si dividimos una unidad en 1.000 partes iguales, cada una de ellas es una milésima.

Cómo hacer una regla (cartulina, madera, balso, etc.) - Matemáticas 3A

Plano cartesiano - repaso (Matemáticas cuarto)

El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.

Las coordenadas se forman asociando un valor del eje de las equis a uno de las yes, respectivamente, esto indica que un punto (P) se puede ubicar en el plano cartesiano tomando como base sus coordenadas, lo cual se representa como:

P (x, y)

Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento:

1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia la izquierda si son negativas, a partir del punto de origen, en este caso el cero.

2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes (en el eje de las ordenadas) hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas ambas coordenadas.

De modo inverso, este procedimiento también se emplea cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano.

• Las variaciones entre dos valores de la variable  independiente y la de sus correspondientes de la variable dependiente son uniformes.

• Todos los puntos de su gráfica están alineados.

Prueba de la multiplicación (Matemáticas 3A)

Para comprobar una multiplicación tenemos varias opciones:

• Volver a realizar la multiplicación para ver si está bien hecha (está opción es la mejor si aún no se sabe dividir). Para comprobar la multiplicación es bueno hacerla nuevamente más lento y si estás en un examen esperar a acabar el examen y volver a hacerla, así el proceso que has hecho no te influenciará tanto en la multiplicación.

• Hacer la prueba de la multiplicación mediante una división: para hacer esto dividiremos el PRODUCTO entre el MULTIPLICADOR y nos tendrá que dar de resultado el MULTIPLICANDO. Si no es así, la multiplicación no estará bien hecha.

A continuación tenemos una tablita que te puede ser muy útil para comprobar si la multiplicación es correcta:

TAREA

Realice las siguientes multiplicaciones con su prueba:

1) 34642x3=

2) 45689x4=

3) 57862x6=

4) 89652x5=

Prismas y pirámides (Geometría 3A)

Los prismas y pirámides son cuerpos geométricos cuyas caras son todas polígonos. Los prismas tienen dos caras paralelas e iguales, llamadas bases, el resto de sus caras son paralelogramos. Las pirámides tienen una base y el resto de las caras son triángulos.

1.1- El prisma
Los prismas son poliedros que tienen:
 
 

 
 
Está constituido por dos bases poligonales e iguales y sus caras laterales son paralelogramos. Según el  número de lados de la base se le da el nombre al prisma.
 
Por ejemplo:  Prismas triangular (sus bases son un triángulo), Prismas cuadrangulares (sus bases son cuadrados) , Prisma pentagonal (sus bases son pentágonos), Prisma hexagonal (sus bases son hexágonos) , etc.
 

 
 
La altura de un prisma es la distancia entre las bases. 

El prisma es  recto cuando su eje es perpendicular a las bases y oblicuo cuando el ángulo entre el eje y la base es diferente a base 90°. Si el prisma es cortado de tal manera que la sección producida no sea paralela a una de sus bases, recibe el nombre de prisma truncado.
 

 

Es una figura tridimensional constituida por una base poligonal y por caras laterales cuyas aristas concurren a un punto del espacio llamado cúspide o vértice común, por lo tanto las caras laterales siempre serán triangulares. El eje o altura de la pirámide es la línea que va del vértice al centro de la base.

En las pirámides, las caras laterales son siempre triángulos. Por tanto, para distinguirlas y nombrarlas se utiliza el polígono de la base.

1.2- La pirámide

La apotema lateral de una pirámide regular es la altura de cualquiera de sus caras laterales.

La pirámide se llama rectangular cuando el eje es perpendicular al centro de la base, en un caso diferente se llama oblicua. La porción de pirámide comprendida entre la base y la sección producida por un plano que corta sus caras laterales se llama tronco de la pirámide o pirámide truncada.

Tipos de pirámides

Fracciones propias e impropias (Matemáticas 3A)

Se llaman fracciones propias a las que el numerador es más pequeño que el denominador:

 

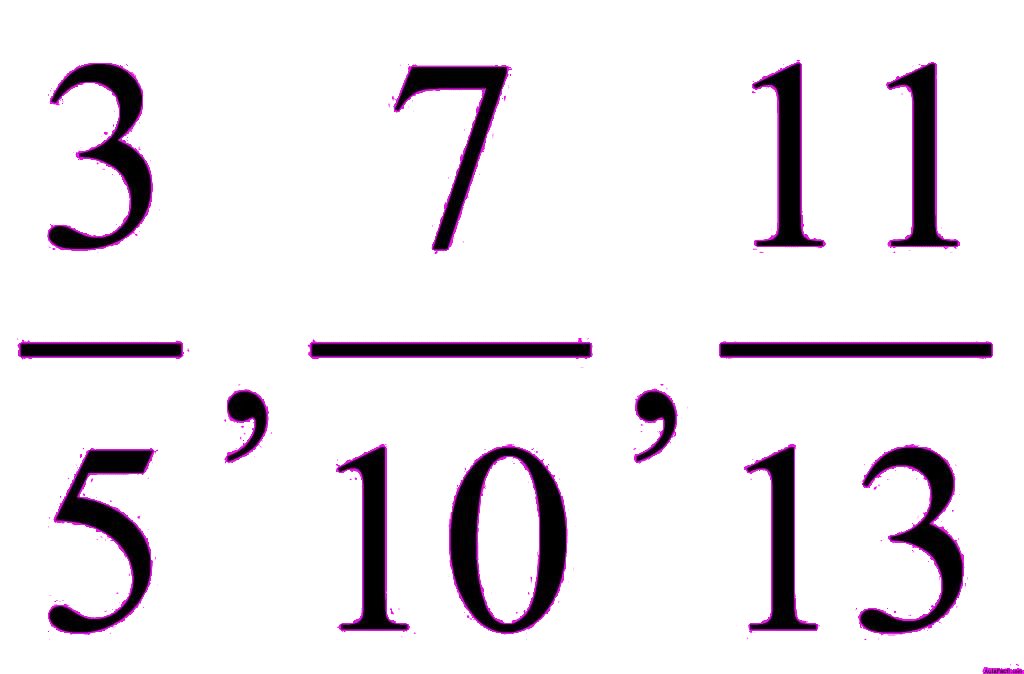
Las impropias son las que el numerador es mayor que el denominador: 

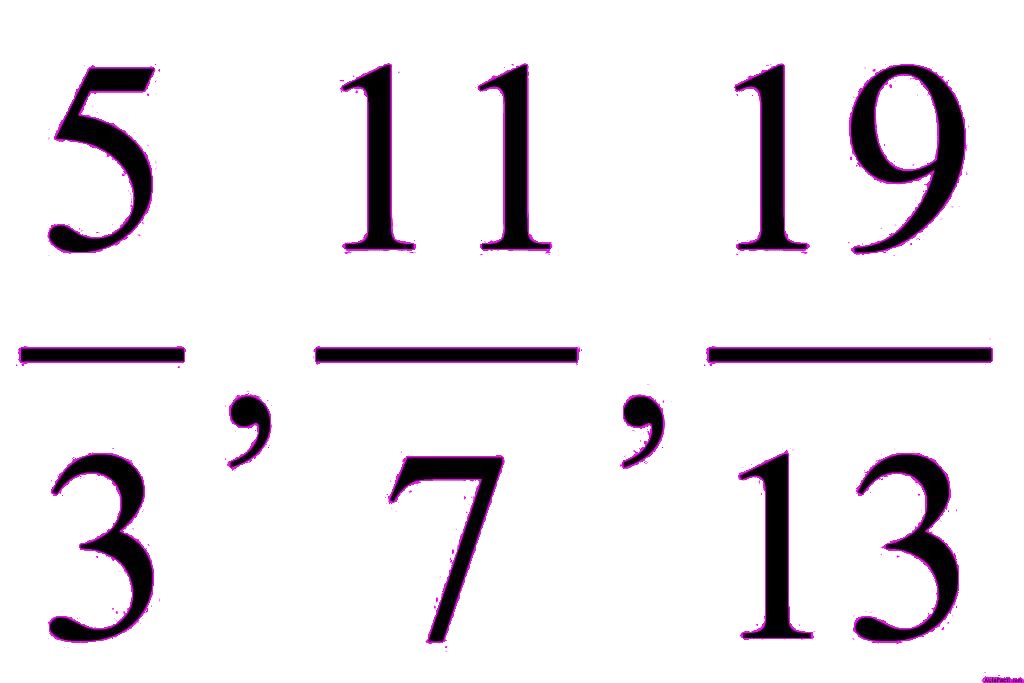
TAREA

1. Escriba 5 fracciones propias.

2. Escriba 5 fracciones impropias.

Fracción de un grupo de objetos (Matemáticas 3A)

Fraccionarios - vídeos para ver en casa (Matemáticas 3A)

Los números romanos: I, V, X, L, C, D, M

¿Sabías que nuestros números vienen del sistema de numeración árabe? ¿Sabías que existen otros sistemas de numeración distintos?

Antes de que los árabes trajesen su sistema de numeración a Europa (y de Europa a América y el resto del mundo), hace mucho tiempo, en la Antigua Roma, los romanos inventaron un sistema de numeración que todavía seguimos utilizando para algunas cosas. Son lo que llamamos números romanos.

¿Cómo se utilizan los números romanos?

Los números romanos están formados a partir de letras: X, L, I, C, D… Cada letra tiene un valor numérico:

Para representar números romanos, debemos utilizar estas letras, combinándolas y ordenándolas. Hay que seguir algunas normas:

• Los símbolos se escriben y leen de izquierda a derecha, de mayor a menor valor.

• Cuando se coloca un símbolo de valor menor a la izquierda de otro, se resta.

• Los símbolos 5 y sus múltiplos (V, L, D) siempre suman y no pueden estar a la izquierda de uno de mayor valor.

• Se permiten como mucho tres repeticiones consecutivas del mismo símbolo.

• Un símbolo que aparece restando solo se puede repetir cuando su repetición esté colocada a más de un símbolo de distancia a su derecha.

• Solo se puede restar un símbolo de tipo 1 (I, X, C, M) sobre el inmediato mayor de tipo 1 o de tipo 5 (V, L, D).

Normas para utilizar correctamente los números romanos:

• El símbolo I solo puede restar a V y a X.
• El símbolo X solo puede restar a L y a C.
• El símbolo C solo puede restar a D y a M.

Después de todas las explicaciones de más arriba, te habrás dado cuenta de que para usar correctamente los números romanos es muy importante saber sumar y restar bien, ¡usamos todo el rato estas dos operaciones cuando escribimos un número romano!

¿Para qué se utilizan los números romanos?

Hoy en día, seguimos utilizando los números romanos para algunas cosas. Por ejemplo, en los siguientes casos:

• Para nombrar los siglos:

Estamos en el siglo XXI

La Revolución francesa ocurrió en el siglo XVIII

Miguel Ángel pintó la Capilla Sixtina en el siglo XVI

• Para nombrar a los reyes:

Fernando II de Aragón se casó con Isabel I de Castilla

El sucesor de Felipe IV fue Carlos II

• Para numerar los tomos o partes de algunos libros o películas:

Ayer vi en la televisión El padrino II

• Para aniversarios, reuniones o festejos que se celebran periódicamente:

El Ayuntamiento está organizando el IV certamen de fotografía juvenil

Polígonos (3A)

Tablas de frecuencia (3A)

División por una cifra.

Aprendamos a dividir por una cifra.